Только надо не скалярное произведение считать, а вычислять знак векторного произведения, знак векторного произведения и будет указывать направлена нормаль к нам или от нас.krt17 писал(а):
Берем 3 точки в одной плоскости и вычисляем скалярное произведение пары получившихся векторов, оно будет определять видимость.
Дизасм Elite
-
Гость
-
Гость
Нет, там точки не обходятся, сразу нормали, обходом эт я думаю переделать. Сейчас подумал, перспектива учитывается не от реального полигона,а от центра, то есть нормали считаются из центра объекта, возможно и влияет. Блин рано делать выводы и предположения, надо все доразобрать.deathsoft писал(а):
Может в модели порядок обхода точек перепутан и из за этого нормаль к грани не в ту сторону повернута.
-
Гость
-
Гость
-
Гость
krt17 писал(а):
Да так и есть, для любого студента тема изи, это просто мы пердуны с закостенелыми мозгами. Разминка нужна, для меня например эта тема.
Шоколадка тошько тогда становится шоколадкой когда ее заворачивают в фантик. Без фантика это субстанция похожая на какашку. Так и разобранная элита без интро скролла и новой ау музыки всего дишь какашка. После оптимитизации обязанетельно надо сделать интро и вставить в эту скучную игру музыку. И еще оставть там только синкляр джойтик а лишние кнопки убрать.
Я вот про это имею ввиду "матрица перехода". В декартовых преобразование координат (когда надо одновременно сделать сдвиг масштабирование и поворот по трем осям) делается немного через жопу, а в однородных - просто домножением матрицы на вектор, причем матрица всего одна.krt17 писал(а):
Немного не так понял, декартовы конечно, почитаю об однородных заодно, вообще забыл.
Так то что нету таблицы синусов совсем не означает что сами синусы не используются, может они там алгоритмом CORDIC считаются. В факте 2 же не написано, что не используются повороты. Может используются повороты на фиксированные углы и заранее посчитаны матрицы поворота для всех значений фиксированных углов, тогда таблицы синусов не будет, будет просто массив матриц и таблица индексов (адресов этих матриц). Как там на спектруме делали я не знаю, но на ПЦ можно было бы сделать так.Отредактировано deathsoft (2016-12-05 00:16:18)krt17 писал(а):
Там углов нет вообще, читаем с факта №2
Проблема не в том, что нормаль не учитывается, но возможно в том что она учитывается не совсем корректно?krt17 писал(а):
Разобрался с нормалями, перспектива учитывается, проблема не в ней
Возможно она учитывается от центра объекта, а нужно от одной из точек грани.
Или другая ошибка в коде, в алгоритме, в выборе точности... так что проблема всё ещё может быть в ней.
Прошу прощения за въедливость, если бы ты написал "проблема не в этом", то я бы не подумал, что что-то может быть упущено.
***
Действительно, вспоминаю, как глядел на пролетающую мимо кобру через боковой обзор. Пролетев середину экрана у неё становилась видимой задняя грань, с соплами. Если-бы перспектива совершенно не учитывалась, то был-бы полный позор.
-
Гость
Разбираюсь потихоньку, решил сделать рендер отдельно, заодно буду проверять таблицу нормалей, просто пересчитаю и сравню с теми что есть. Я уже писал что перспектива учитывается но только относительно глобальных координат, то есть рендеру смещение полигона от центра модели уже пофигу. Там есть еще не совсем понятный момент с масштабированием нормали, этот масштаб глобальный для модели. Кстати то что я называю вектором нормали не совсем верно, это z компоненты матрицы поворота  просто как то так в голове назвалось.
просто как то так в голове назвалось.
 просто как то так в голове назвалось.
просто как то так в голове назвалось.-
Гость
Посидел с утра, начал имитацию рендера.

Понял откуда масштабирование нормали и как учитывается смещение от центра. Грубо говоря нормаль высчитывается от точки центра модели плюс смещение по направлению нормали с определенным для модели масштабом. То есть типа сфера, на ней точка и к ней уже применяется перспектива. Самые объемные питон и станция.

Понял откуда масштабирование нормали и как учитывается смещение от центра. Грубо говоря нормаль высчитывается от точки центра модели плюс смещение по направлению нормали с определенным для модели масштабом. То есть типа сфера, на ней точка и к ней уже применяется перспектива. Самые объемные питон и станция.
Свой тестовый отрисовщик, это хорошо. Капитальный подход.
Смотрю на нормали, они подряд #6B,#6B,#6B (октаэдрические грани). Знаки наверное в четвёртом байте запрятаны.
А кубоидные грани #00,#00,#A0
Построил в Компасе куб размером 160 (#A0), делаю октаэдрические грани из точки (107,107,107)=(#6B,#6B,#6B) - получается похоже.
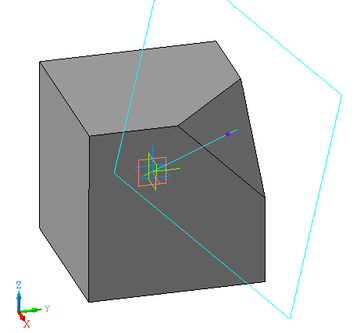 Отредактировано Reobne (2016-12-09 03:20:06)
Отредактировано Reobne (2016-12-09 03:20:06)
Смотрю на нормали, они подряд #6B,#6B,#6B (октаэдрические грани). Знаки наверное в четвёртом байте запрятаны.
А кубоидные грани #00,#00,#A0
Построил в Компасе куб размером 160 (#A0), делаю октаэдрические грани из точки (107,107,107)=(#6B,#6B,#6B) - получается похоже.
 Отредактировано Reobne (2016-12-09 03:20:06)
Отредактировано Reobne (2016-12-09 03:20:06)-
Гость
Решил потестить точность и правильность короткого умножения.
В EmuZWin написал небольшой тест
Код: org #4000entrypoint $diLD BC,512loopcall #e434OUT(#FE),Ainc cjp nz,loopinc bjp nz,loopexit haltjp exit
откомпилировал, и сохранил состояние в формате *.Z80.
В DelphiSpec добавил при выводе в порт 254 код
Код: frmRam.Log.Lines.Append(IntToStr(regB)+#9+IntToStr(regC)+#9+IntToStr(regA*256)+#9+IntToStr(regB*regC)+#9+IntToStr(regB*regC-regA*256));
прогнал сохранюшку, и перекопировал результат в Ексель, и там посортировал и поанализировал.
Результат: процедура работает относительно стабильно - гиганской погрешности в некоторых "пасхальных" сочетаниях не выявлено.
Наибольшие пики абсолютной погрешности лежат в области значений обоих множителей больше 200.
B
C
A*256
B*C
Погрешность
Относительная п
241
242
57856
58322
466
0.0079901
240
243
57856
58320
464
0.0079561
234
235
54528
54990
462
0.0084015
Не идеально, но более-менее. Относительная погрешность в этих пиках меньше процента.
Максимальные относительные погрешности - наоборот, на небольших значениях множителей.
B
C
A*256
B*C
Погрешность
Относительная п
31
1
256
31
-225
7.258
32
1
256
32
-224
7
45
1
256
45
-211
4.6889
Результат умножения не равномерный. 31*1=256, 32*1=256, а с 33 по 44 получаются нули.
Вот такие флуктуации и квантовые эффекты на низком уровне вселенной Элиты.
В EmuZWin написал небольшой тест
Код: org #4000entrypoint $diLD BC,512loopcall #e434OUT(#FE),Ainc cjp nz,loopinc bjp nz,loopexit haltjp exit
откомпилировал, и сохранил состояние в формате *.Z80.
В DelphiSpec добавил при выводе в порт 254 код
Код: frmRam.Log.Lines.Append(IntToStr(regB)+#9+IntToStr(regC)+#9+IntToStr(regA*256)+#9+IntToStr(regB*regC)+#9+IntToStr(regB*regC-regA*256));
прогнал сохранюшку, и перекопировал результат в Ексель, и там посортировал и поанализировал.
Результат: процедура работает относительно стабильно - гиганской погрешности в некоторых "пасхальных" сочетаниях не выявлено.
Наибольшие пики абсолютной погрешности лежат в области значений обоих множителей больше 200.
B
C
A*256
B*C
Погрешность
Относительная п
241
242
57856
58322
466
0.0079901
240
243
57856
58320
464
0.0079561
234
235
54528
54990
462
0.0084015
Не идеально, но более-менее. Относительная погрешность в этих пиках меньше процента.
Максимальные относительные погрешности - наоборот, на небольших значениях множителей.
B
C
A*256
B*C
Погрешность
Относительная п
31
1
256
31
-225
7.258
32
1
256
32
-224
7
45
1
256
45
-211
4.6889
Результат умножения не равномерный. 31*1=256, 32*1=256, а с 33 по 44 получаются нули.
Вот такие флуктуации и квантовые эффекты на низком уровне вселенной Элиты.
-
Гость
Там еще есть такой момент что числа хранятся со знаком и при умножении во многих местах перед этим умножаются на 2, это часто спасает формулу. Рендер я почти доделал, но очень не удобно пока управлять поворотом, ортогональные базисы в ручную не забьешь, надо крутилку придумать.
Там рядом есть hl=b*c лучше его проверить. Еще вспомнил что базис нормируют на всякий случай, пока до разбора детального этой части не дошел, наверное еще что то есть ибо погрешности по любому накопятся.Отредактировано krt17 (2016-12-17 09:39:22)
Там рядом есть hl=b*c лучше его проверить. Еще вспомнил что базис нормируют на всякий случай, пока до разбора детального этой части не дошел, наверное еще что то есть ибо погрешности по любому накопятся.Отредактировано krt17 (2016-12-17 09:39:22)
Хорошо. Иду по проторенной дорожке.krt17 писал(а):
Там рядом есть hl=b*c
"call #e434" заменил на "call #e45d";
"RegA*256" на "RegHL".
Обе процедуры умножения не портят BC.
Смотрю результат в екселе.
С вероятностью 0.5 погрешность нулевая.
Это происходит, когда (B xor C)and 1 = 0; то есть когда оба множителя чётные или оба нечётные.
Если один множитель чётный, а другой нечётный, то происходит "недобор" значения произведения на величину меньшего множителя.
Например 10*11=>100; 19*10=>180.
Из этого получается, что максимальные абсолютные погрешности происходят, когда оба множителя большие; но при этом относительная погрешность меньше процента 200*255=>51000-200.
Максимальная-же относительная погрешность: 1*2=>2-1=1; пятьдесят процентов, но абсолютная погрешность при этом всего единичка.
Никаких пасхалок на всём диапазоне входных значений нет. Процедура стабильна в пределах описанной погрешности.
Короче говоря, я ещё не понял, где могут быть такие сбои, что грани проподают-появляются. Но есть ещё несколько идей, где можно поискать.
-
Гость
Лазил по инету осматривая на предмет элит, набрел на жава версию http://www.elite-games.ru/downloads/elite/jvelite.rar . В ней есть модели кучи кораблей, формат немного другой но можно конвертировать, при этом сами координаты совпадают на 100%. Возможно пригодится.
-
Гость
-
Гость
Ну так то есть, но пока крутить неудобно, я ортогональные базисы из головы не могу выписывать:). И для моделей тоже конвертер нужен, там принцип хранения граней немного другой, я жеэс с такой скоростью выдавать не навострился еще.dr.Titus писал(а):
Ну у тебя же есть крутилка кораблей, что несколько скриншотами выше.
По простому, рассматривая этот базис как матрицу, умножаем её на грубую матрицу вращения:krt17 писал(а):
я ортогональные базисы из головы не могу выписывать:).
1
rZ
rY
-rZ
1
rX
-rY
-rX
1
А потом ортонормируем, рассматривая базис как три вектора:
V1:=V1/abs(V1)
V2:=ort(V2,V1)
V2:=V2/abs(V2)
V3:=ort(ort(V3,V1),V2)
V2:=V2/abs(V2)
Где abs(V)=SQRT(V.X^2+V.Y^2+V.Z^2)
ort(V1,V2)=V1-V2*(V1*V2); (расшифровка: от вектора1 отнимается вектор2 умноженный на скалярное произведение этих векторов)
Таблицы Normals, Points и Edges точнее было-бы назвать Planes, Nodes и Edges.
-
Гость
Красавчик, как в теории делать я представлял, но расписывать было лениво, сделаю временно так. Опять же, стараюсь повторить как сделано в коде, а там у меня мозги быстро плывут от обилия индексов и перестановок по регистрам. Там ортонормируют но возможно порядок другой.Reobne писал(а):
А потом ортонормируем
-
Гость
Ну я думаю уже желающие могут покруть сами http://rgho.st/6hwPWGymt
За говнокод извиняйте, хотелось побыстрее запустить, не до красот.
За говнокод извиняйте, хотелось побыстрее запустить, не до красот.


