глупость конечно, но я писал для себя и надеюсь, кому нибудь это поможет.
https://e-maxx.ru/algo/circle_line_intersection
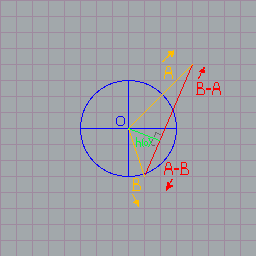
задача найти точки пересечения прямой и окружности. пусть будет 2 вектора A и B,
между ними прямая. начало координат - круг радиусом r.
уравнение прямой x*d - y*e = c
c = A^B = Ax*By - Ay*Bx
d = Ay-By
e = Ax-Bx (или вектор A-B)
или наоборот
c` = B^A = Bx*Ay - By*Ax
d` = By-Ay
e` = Bx-Ax (или вектор B-A)
disk.yandex.ru/i/nINhIYk2fO1K2w
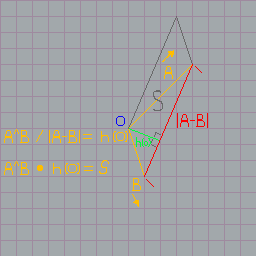
ближайшее расстояние от прямой до центра:
S/|A-B|*2=h(O)
где h(O) - высота треугольника из начала координат, S - прощадь, |A-B|
расстояние между векторами A, B
но так как abs(c`)=abs(c)=S*2, высота параллелограмма
abs(c`)/|A-B|=abs(c)/|A-B|=h(O)=g
если g больше r, значит точек пересечения нет.
disk.yandex.ru/i/ptK2FCSD9eX4QQ
координаты точки:
поворот вектора на 90, -90 градусов
Fx = cos({90,-90})*x - sin({90,-90})*y = {0,0}*e - {1,-1}*d
Fy = cos({90,-90})*y + sin({90,-90})*x = {0,0}*d + {1,-1}*e
disk.yandex.ru/i/f2bz1rUeUgW-yg
что в сути, нужно менять только знак. так как с=A^B, а A^B/(|A|*|B|) = sin(A,
B) - знак уже есть (!!! очень странное объяснение, c может и не быть
A^B !!!). g=abs(c)/|A-B|, ещё одно деление на |A-B|, чтобы масштабировать до g.
Fx = -c/|A-B|/|A-B|*d = -c*d/|A-B|^2
Fy = c/|A-B|/|A-B|*e = c*e/|A-B|^2
(для Fx` и Fy` поменять c,d,e на c`,d`,e`)
если g=r, значит F и есть единственная точка.
disk.yandex.ru/i/PNmpYapB41UWUg
есть диагональ прямоугольника r2 (его половина это описанная окружность) и
сторона g*2, нужно найти j/2 (расстояние точек соприкасания с окружностью, от
ближайшей точки до центра).
sqrt((g*2)^2+j^2)/2 = r ->
sqrt((r*2)^2-(g*2)^2) = j ->
sqrt((r*2)^2-(g*2)^2)/2 = j/2 = sqrt(r^2 - g^2)
и координаты:
F0x = Fx - j/2/|A-B|*e = Fx - sqrt((j/2)^2 / A*B)*e
F0y = Fy - j/2/|A-B|*d
F1x = Fx + j/2/|A-B|*e
F1y = Fy + j/2/|A-B|*d
знакомый научный работник (ретро-геймер из вк) сказал, что нужно отсылку к пифагору, иначе не опубликуют в сайнс. смысл этого тоже, весьма зыбок. как оказалось, но это уже тема для другой статьи. забиваю блант, отбиваю рюмку. владимир путин посетеил с визитом туалет - из колонок играет. доказательств не будет, потому что мне срать из жопы говном. но если найдёте ошибки - сообщите. картинки сами смотрите, форум запрещает их постить (больше одной).
расшифровка статьи про пересечение отрезка с окружностью
расшифровка статьи про пересечение отрезка с окружностью
Последний раз редактировалось lenin1st 12 фев 2022, 09:12, всего редактировалось 1 раз.
а что такое угол отрезка? угол луча неизвестный.
а ну да, только как масштабировать... щас я не очень в теме. в любом случае, это не то чтобы полезная вещь (мне), просто разбирал для себя что автор имел ввиду.
а ну да, только как масштабировать... щас я не очень в теме. в любом случае, это не то чтобы полезная вещь (мне), просто разбирал для себя что автор имел ввиду.
Последний раз редактировалось lenin1st 17 фев 2022, 15:05, всего редактировалось 1 раз.
расшифровка статьи про пересечение отрезка с окружностью
расшифровка статьи про пересечение отрезка с окружностью перенес сюда в программирование, а то ишь ты расслабились!